XGBoost conocido como Extreme Gradient Boosting (Potenciación del gradiente) es una técnica de aprendizaje automático utilizado para el análisis de la regresión)
Descargamos el dataset bike_rentals_cleaned.csv, he eliminado valores N/As y columnas que no sean independientes de la variable objetivo. Por ejemplo, cnt: conteo total de las bicicletas alquiladas es la suma de las columnas: casual y registrados (tipos de usuario)
Una descripción general del dataset en cuestión puede ser la siguiente:
- instant: índice de registro
- dteday : fecha
- season : temporada (1:invierno, 2:primavera, 3:verano, 4:otoño)
- yr : año (0: 2011, 1:2012)
- mnth : mes (1 a 12)
- hr : hora (0 a 23)
- holiday: el día meteorológico es feriado o no
- weekday: día de la semana
- workingday: si el día no es fin de semana ni festivo es 1, de lo contrario es 0.
- weathersit
- 1: Despejado, Pocas nubes, Parcialmente nublado, Parcialmente nublado
- 2: Niebla + Nublado, Niebla + Nubes rotas, Niebla + Pocas nubes, Niebla
- 3: Nieve ligera, Lluvia ligera + Tormenta eléctrica + Nubes dispersas, Lluvia ligera + Nubes dispersas
- 4: Lluvia Pesada + Paletas de Hielo + Tormenta Eléctrica + Niebla, Nieve + Niebla
- temp : Temperatura normalizada en Celsius. Los valores se obtienen mediante (t-t_min)/(t_max-t_min), t_min=-8, t_max=+39 (solo en escala horaria)
- atemp: temperatura de sensación normalizada en Celsius. Los valores se obtienen a través de (t-t_min)/(t_max-t_min), t_min=-16, t_max=+50 (solo en escala horaria)
- hum: Humedad normalizada. Los valores se dividen en 100 (máx.)
- windspeed: Velocidad del viento normalizada. Los valores se dividen en 67 (máx.)
- casual: cuenta de usuarios casuales
- registered: número de usuarios registrados
- cnt: recuento del total de bicicletas de alquiler, incluidas las ocasionales y registradas
Empecemos a programar
Cargar librerías
Instalamos las librerías necesarias directamente desde un arquivo de requisitos: requirements.txt
!pip install -r requirements.txt
Verificamos la versión de las librerías a utilizar
import platform; print(platform.platform())
import sys; print("Python", sys.version)
import numpy; print("NumPy", numpy.__version__)
import scipy; print("SciPy", scipy.__version__)
import sklearn; print("Scikit-Learn", sklearn.__version__)
import xgboost; print("XGBoost", xgboost.__version__)
import pandas as pd; print("Pandas", pd.__version__)
La configuración que he utilizado es la siguiente:
Linux-5.4.144+-x86_64-with-Ubuntu-18.04-bionic
Python 3.7.12 (default, Jan 15 2022, 18:48:18)
[GCC 7.5.0]
NumPy 1.21.5
SciPy 1.4.1
Scikit-Learn 1.0.2
XGBoost 0.90
Pandas 1.3.5
Importar el dataset
Leemos el dataset desde un CSV podría ser un xlsx (Excel) o similar.
df_bicicletas = pd.read_csv('bike_rentals_cleaned.csv')
Analizamos el DataFrame
Observemos
f_bicicletas.head()
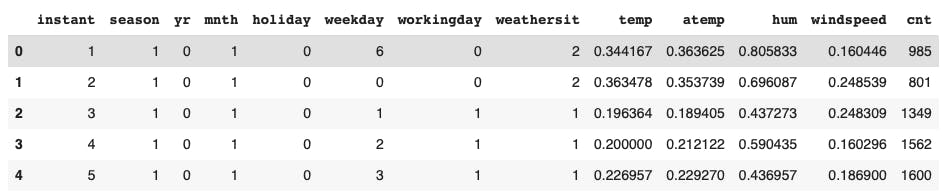
Veamos la "forma" de nuestro DataFrame
df_bicicletas.shape
(731, 15)
Análisis descriptivo del dataset
df_bicicletas.describe()

Analizamos cada columna
df_bicicletas.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 731 entries, 0 to 730
Data columns (total 15 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 instant 731 non-null int64
1 season 731 non-null int64
2 yr 731 non-null int64
3 mnth 731 non-null int64
4 holiday 731 non-null int64
5 weekday 731 non-null int64
6 workingday 731 non-null int64
7 weathersit 731 non-null int64
8 temp 731 non-null float64
9 atemp 731 non-null float64
10 hum 731 non-null float64
11 windspeed 731 non-null float64
12 casual 731 non-null int64
13 registered 731 non-null int64
14 cnt 731 non-null int64
dtypes: float64(4), int64(11)
memory usage: 85.8 KB
Regresión Lineal Múltiple
Variable a predecir: cnt Numero de bicicletas alquiladas
df_bicicletas['cnt']
0 985
1 801
2 1349
3 1562
4 1600
...
726 2114
727 3095
728 1341
729 1796
730 2729
Name: cnt, Length: 731, dtype: int64
Dividimos el dataset en preditores (features) y variable a predecir
X = df_bicicletas.iloc[:,:-1]
y = df_bicicletas.iloc[:,-1]
Importamos ( por facilidad) un módulo para dividir en train/test aunque se podría realizar manualmente
from sklearn.model_selection import train_test_split
Importamos módulo de regresión lineal
from sklearn.linear_model import LinearRegression
Dividimos en train/set
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=26)
Nota: Utilizaremos random_state= 26 para la reproducibilidad del procedimiento. Ver mecanismos de generación de números pseudoaleatorios
Instanciamos el modelo
lin_reg = LinearRegression()
Hacemos el fit del modelo sobre nuestros datos de train
lin_reg.fit(X_train, y_train)
Realizamos predicciones sobre nuestra partición de test
y_pred = lin_reg.predict(X_test)
Calculando métricas de error
Importamos el módulo de RSME (Raíz del error cuadrático medio)
from sklearn.metrics import mean_squared_error
La RECM de un estimador con respecto al parámetro estimado , se define como la raíz cuadrada del error cuadrático medio:
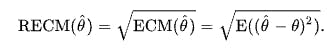 Para un estimador insesgado, la RECM es la raíz cuadrada de la varianza, conocida como desviación estándar.
Para un estimador insesgado, la RECM es la raíz cuadrada de la varianza, conocida como desviación estándar.
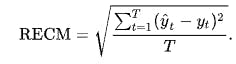
Importamos numpy para realizar cálculos
import numpy as np
Calculamos el MSE
mse = mean_squared_error(y_test, y_pred)
Calculamos el RSME
rmse = np.sqrt(mse)
Observamos la raíz cuadrada del error cuadrático medio de nuestro modelo
print("RMSE: %0.4f" % (rmse))
RMSE: 898.3256
Observemos la naturaleza de nuestra variable a predecir y para saber que tan bueno ( o malo) es nuestro modelo.
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
bike_num=df_train[[ 'temp', 'atemp', 'hum', 'windspeed','cnt']]
sns.pairplot(bike_num, diag_kind='kde')
plt.show()
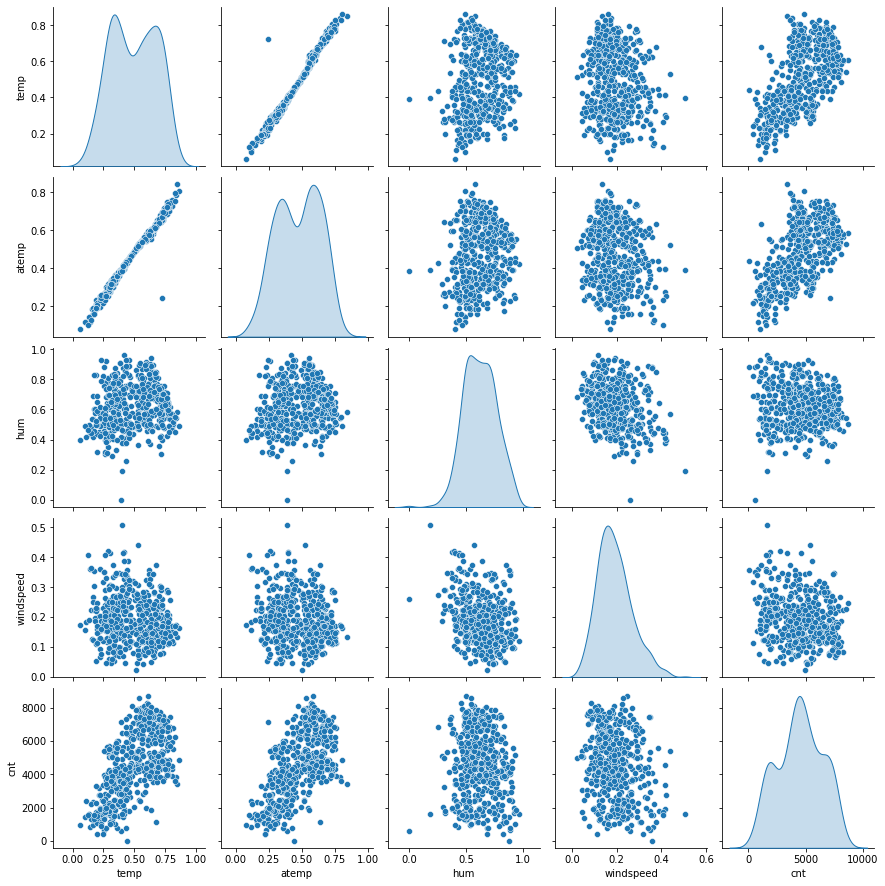
Otro gráfico interesante puede ser la correlación entre atemp( temperatura de sensación normalizada) y cnt (variable objetivo)
from matplotlib.ticker import FormatStrFormatter
# Create Fig and gridspec
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(16, 10), dpi= 80)
grid = plt.GridSpec(4, 4, hspace=0.5, wspace=0.2)
# Define the axes
ax_main = fig.add_subplot(grid[:-1, :-1])
ax_right = fig.add_subplot(grid[:-1, -1], xticklabels=[], yticklabels=[])
ax_bottom = fig.add_subplot(grid[-1, 0:-1], xticklabels=[], yticklabels=[])
df = df_bicicletas
# Scatterplot on main ax
ax_main.scatter('atemp', 'cnt', s=df.atemp*200, c=df.workingday.astype('category').cat.codes, alpha=.5, data=df, cmap="tab10", edgecolors='gray', linewidths=.5)
# histogram on the right
ax_bottom.hist(df.atemp, 40, histtype='stepfilled', orientation='vertical', color='deeppink')
ax_bottom.invert_yaxis()
# histogram in the bottom
ax_right.hist(df.cnt, 40, histtype='stepfilled', orientation='horizontal', color='deeppink')
# Decorations
ax_main.set(title='Scatterplot with Histograms \n atemp vs cnt', xlabel='atemp', ylabel='cnt')
ax_main.title.set_fontsize(20)
for item in ([ax_main.xaxis.label, ax_main.yaxis.label] + ax_main.get_xticklabels() + ax_main.get_yticklabels()):
item.set_fontsize(14)
xlabels = ax_main.get_xticks().tolist()
ax_main.set_xticklabels(xlabels)
ax_main.xaxis.set_major_formatter(FormatStrFormatter('%.2f'))
plt.show()

df_bicicletas['cnt'].describe()
count 731.000000
mean 4504.348837
std 1937.211452
min 22.000000
25% 3152.000000
50% 4548.000000
75% 5956.000000
max 8714.000000
Name: cnt, dtype: float64
Entonces un RSME de 898 con una desviación típica de 1937 y media de 4504 para no ser tan malo. Revisemos el ajuste R cuadado
Importamos el módulo siguiente
from sklearn.metrics import r2_score
Calculamos el R Cuadrado
print("R Cuadrado: ", r2_score(y_test, y_pred))
R Cuadrado: 0.7932467888971358
79,32% ... Seguro podemos mejorarlo
XGBRegressor
Importamos:
from xgboost import XGBRegressor
Inicializamos el modelo
xg_reg = XGBRegressor()
Hacemos el fit del modelo sobre nuestros datos de train
xg_reg.fit(X_train, y_train)
Predicción sobre nuestra partición de test
y_pred = xg_reg.predict(X_test)
Calculamos nuevamente las métricas de error
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
print("RMSE: %0.2f" % (rmse))
RMSE: 638.21
R Cuadrado: 0.895645596385285
Perfecto! Hemos reducido el RMSE y ahora tenemos un R Cuadrado de 89.56%
Pero todavía podemos mejorar nuestro modelo...
Cross-validation
La validación cruzada o cross-validation es una técnica utilizada para evaluar los resultados de un análisis estadístico y garantizar que son independientes de la partición entre datos de entrenamiento y prueba. Consiste en repetir y calcular la media aritmética obtenida de las medidas de evaluación sobre diferentes particiones.
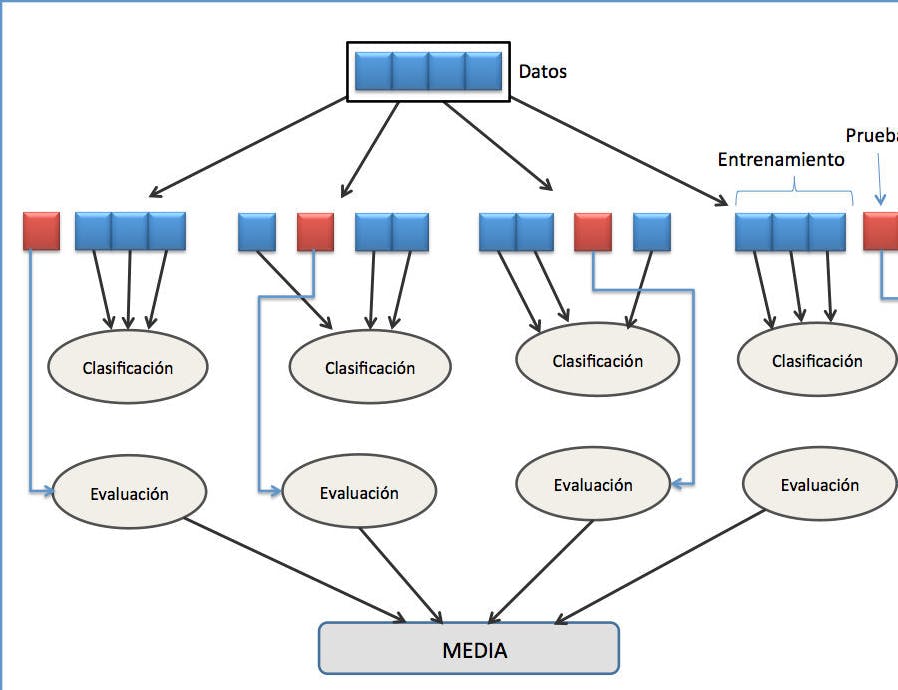
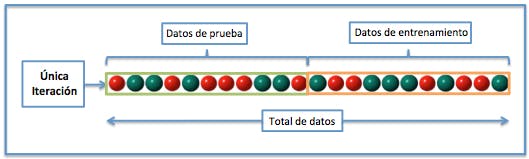
Validación cruzada con XGBoost
Inicializamos el modelo
model = XGBRegressor()
Definitimos la métrica de scoring Nota: Ignoremos los warnings
scores = cross_val_score(model, X, y, scoring='neg_mean_squared_error', cv=100)
Calculamos el error
rmse = np.sqrt(-scores)
print('Reg rmse:', np.round(rmse, 2))
print('RMSE mean: %0.2f' % (rmse.mean()))
Reg rmse: [ 464.69 178.26 253.69 496.79 254.91 166.35 355.4 217.04 429.27
334.11 313.36 503.95 462.62 858.68 481.82 416.64 478.72 375.61
376.79 253.41 276.45 481.81 321.25 627.28 528.01 390.38 458.07
272.04 431.67 1044.28 346.95 815.44 308.96 890.3 341.15 449.48
536.29 462.14 575.88 489.45 584.49 365.06 1092.62 244.22 595.79
219.32 1390.46 841.37 552.64 545.29 503.64 685.92 315.64 483.85
364.12 539.18 788.38 603.36 863.5 1249.62 598.7 710.54 403.48
1035.57 634.93 563.5 1116.21 657.82 463.67 1020.03 347.03 470.66
464.39 631.63 824.77 365.95 690.52 487.66 498.34 600.28 1119.76
348.04 544.64 497.38 365.09 599.56 329.53 967.35 789.37 835.99
1588. 1264.8 466.78 333.72 1965.75 674.63 842.36 530.39 872.41
864.52]
RMSE mean: 589.34
Perfecto! Finalmente hemos reducido el RMSE a 589.34